Tag Archives: illustration

The ‘Long 2s’ Of Financial Markets

Summary In honor of the closure of Grantland, an application of sports analytics to portfolio management. In basketball, a long two-point shot is inefficient with a low average return and high variance of returns. This article looks at three similar investment classes in financial markets that similarly produce lower expected returns over time. The news late Friday of ESPN’s shuttering of sports and pop culture website Grantland was disheartening. I liked the mix of long-form journalism and irreverent pop culture topics from a diverse array of skilled young writers, but particularly I loved the articles on deep, and often arcane, sports analytics. As someone with post-graduate studies in analytic finance, the combination of Big Data and some of America’s pastimes spoke to me. Growing up in basketball-crazed Indiana, the articles from Grantland’s Kirk Goldsberry and Zach Lowe allowed me to watch a game I have had a life-long passion for in new and unique ways. One of the simplest and most frequent basketball-related discussion was the inefficiency of the “Long 2”, two-point field goal attempts from just inside the three-point line. A slightly above-average 3-point shooter making 40% of his shots could more than offset a skilled big man making 55% percent of his shots close to the basket. The 1.2 points-per-shot from the 3-point specialist outscored the 1.1 points-per-shot from the post player. The 3-point shooter will score more points on average over time, but of course, sample sizes are not unlimited in a came with a clock. Borrowing from finance, the three-point shooter has higher average returns, but more variable returns from the more difficult shots. If those long shots are not going in with enough frequency, a more steady point scorer can outperform over shorter stretches of time. Now imagine a jump shooter who typically takes long two-point shots, and makes 45% of the shots on average, more than the 3-pt shooter but less than the close range scorer. That shooter scores just 0.9 points per shot. Basketball coaches have realized these shots are inefficient. For investors, these long two point shots with lower expected returns per unit of risk can be said to be below the efficient frontier. In the spirit of Grantland and the inefficiency of the Long 2, I am going to cover three equivalencies in the world of finance, investments that do not offer requisite returns for their relative riskiness. Low Rated Junk Bonds When we learn the Capital Asset Pricing Model in school, we are taught that required returns are proportional to an asset’s (non-diversifiable) risk. The limits of this model can be seen on a basketball court. As you move further away from the basket, your shooting percentage is not going to fall linearly. If you hit 80% of your free throws from 15 feet away from the basket, you are less likely to hit 40% from 30 feet from the basket (8 feet behind the NBA 3-point line) and are even less likely to hit 20% from 60-feet from the basket, or two-thirds of length of a professional court. This analogy can be applied to the debt of corporations. Imagine you are getting paid 5% returns to lend to a company with leverage (Debt/EBITDA) of 3 times. Even if yields paid to investors did rise linearly per unit of leverage (they do not), if you expected to earn 15% returns lending to companies with nine times as much debt as their earnings, you are employing a strategy akin to shooting sixty-footers every time down the court. The only exception is in this example, you can actually see points reduced from your scoreboard in the likely scenario that the 9x levered company goes bankrupt, liquidates its assets, and pays a recovery to bondholders less than the price at which you purchased the securities. Over long-time intervals, it has been shown that buyers of BB-rated bonds (the highest quality junk bonds) outperform buyers of lower rated, higher yielding single-B and CCC-rated bonds. You just aren’t getting paid enough for those more risky shots. For additional evidence of this phenomenon, see: The Low Volatility Anomaly: A High Yield Bond Example or The Winning Trade in High Yield Corporate Bonds High Dividend Stocks Research has shown that stocks paying dividend yields between three to six percent produce higher absolute returns than stocks with yields above six percent. Dividend yields above this threshold are usually a function of lower stock prices and not necessarily higher payouts as the market begins to reflect concerns about the company’s business profile. Companies that are generating enough stable cash flow to support this dividend level could also be signaling to the market that they do not have sufficient internal investments to drive the value of the firm prospectively. S&P 500 companies that have dividend yields above this 6% threshold include businesses from the secularly declining wireline telecom industry – Frontier Communication (NASDAQ: FTR ) and CenturyLink (NYSE: CTL ). Seagate Technology (NASDAQ: STX ), a make of hard drives, would also fit into this declining business model archetype. To me these types of stocks are the Kobe Bryant’s of the investing world. CenturyLink delivered 30% annual returns from 1995-1999. Frontier put up an MVP-like 77% return in 1999. Seagate averaged 20% returns from 2003-2007. These are former all-stars, but their best days may well be behind them. Investors attracted to the flashy dividend yield may see a star, but not recognize that the future is not nearly as bright as the past. For additional evidence on the relative underperformance of high dividend yielding stocks: The Dividend Sweet Spot High Beta Stocks One of my most common themes on Seeking Alpha has been the Low Volatility Anomaly, or why lower risk investments have outperformed their higher risk cohorts. An example of this phenomenon was discussed in the junk bond/sixty-footer analogy. Across markets, geographies, sectors, and time, lower volatility investments have produced higher returns per unit of risk than higher beta investments. Similarly, there have been plenty examples of all-star laden teams that failed to have sustainable success where more disciplined teams have generated surprising outperformance. In 2014-2015, Gordon Hayward (formerly of those great overachieving Butler Bulldog teams) and DeMarre Carroll, the only member of the unexpectedly excellent Atlanta Hawks not named to the All-Star team, both averaged 1.35 points-per-shot. This figure just trailed the performance of LeBron James (1.36 points-per-shot), arguably the best player on the planet. If the NBA were a market exchange, LeBron would likely be the highest priced commodity, but two players who combined last year earned less than LeBron (who is likely vastly underpaid given the salary cap construct) produced similar levels of efficient play by one measure. Low volatility stocks are mis-priced because investors prefer the spectacular alley-oop to good ball movement and an efficient corner three. For more detailed information on why Low Volatility Stocks outperform: 5 Ways to Beat the Market: Part-3 Revisited Those closely guarded pull-up long 2s can be spectacular to watch, but as Grantland showed us, they do not lead to long-run winning performance. Hopefully, this illustration of the Long 2’s of finance can help Seeking Alpha readers build more efficient portfolios.

Using Leverage To Get More Out Of Your Bond Allocation

Summary A 50/50 stocks and bonds portfolio typically generates better risk-adjusted returns than a stocks-only portfolio. This is because bond funds generate positive alpha. For an S&P 500 index fund paired with an uncorrelated bond fund, the net beta is 0.5 and the net alpha is one-half the bond fund’s alpha. An easy way to improve raw and risk-adjusted returns is to allocate one-sixth to a 3x S&P 500 fund, and five-sixths to the bond fund. The portfolio beta is still 0.5, but portfolio alpha is five-sixths rather than one-half of the bond fund’s alpha. The strategy generalizes to asset allocations other than 50/50 and allows for non-zero correlation between the bond fund and the S&P 500. Fixed Stock/Bond Portfolios Personal investors typically increase exposure to bonds as they get closer to retirement, reducing risk and drawdown potential while also sacrificing raw returns. Consider a 50% stocks, 50% bonds portfolio based on a simple S&P 500 index fund and a total bond mutual fund or ETF. The beta for such a portfolio is simply the average beta of the two funds. If there is no correlation between the two funds, the portfolio beta is 0.5. That means it tends to move 0.5% for every 1% the S&P 500 moves, which of course reduces both growth potential and drawdown potential. The portfolio alpha for a 50/50 strategy is one-half the bond fund’s alpha. So if the bond fund has positive alpha due to maturing bonds and/or falling interest rates, the portfolio will have positive alpha. This is unlike a 100% S&P 500 portfolio, which by definition has zero alpha. Notably, net positive alpha is the reason that portfolios with both stocks and bonds generally have better risk-adjusted returns than portfolios with only stocks. If bond funds didn’t generate positive alpha, you’d be better off allocating a fixed percentage to cash rather than bonds to reduce your portfolio’s beta. The same logic here applies to asset allocations other than 50/50. For example, the net alpha and beta for a 20% S&P 500, 80% total bond fund would be four-fifths the bond fund’s alpha and 0.2, respectively. Again, we are assuming zero correlation between the two funds for the moment. Fixed Stock/Bond Portfolios With Leverage A common approach to achieve a net beta of 0.5 is to allocate 50% of assets to an S&P 500 fund, and 50% to a bond fund. But we can gain a notable advantage by using a leveraged S&P 500 fund to achieve the same beta. If we used a 3x daily S&P 500 fund, we would need to allocate 16.67% of assets to the 3x fund and the remaining 83.33% to the bond fund. Our portfolio beta is still 0.5, but our portfolio alpha is now five-sixths (rather than one-half) the bond fund’s alpha. A higher alpha for the same 0.5 beta translates to better raw and risk-adjusted returns. A More General Framework Suppose you wish to achieve some target beta by combining a leveraged S&P 500 fund and a particular bond fund. Let a represent the allocation to the leveraged S&P 500 fund. This is what we want to calculate. Let b represent the bond fund’s beta. Let c represent the leveraged fund’s target multiple. Let beta represent your desired portfolio beta. The necessary allocation to the leveraged fund is given by: a = ( b eta – b ) / ( c – b ) For a concrete example, suppose we wanted to use ProShares UltraPro S&P 500 (NYSEARCA: UPRO ), a 3x daily S&P 500 ETF, and Vanguard Total Bond Market ETF (NYSEARCA: BND ), to achieve a portfolio beta of 0.75. For b , I’ll use BND’s beta since inception, which is -0.035. Our target beta is 0.75 and c is UPRO’s leverage multiple, which is 3. a = (0.75 – -0.035) / (3 – -0.035) = 0.259. So we need to allocate 25.9% of our assets to UPRO, and the remaining 74.1% to BND. By doing so, we’ll retain 74.1% of BND’s alpha (which is 0.0191%). If we had used SPY rather than UPRO, we would have retained only 24.1% of BND’s alpha. The portfolio alphas would be 0.0142% and 0.0046%, respectively. Practical Considerations The main drawback of my approach is that it requires more frequent re-balancing to maintain a target asset allocation. This translates to more trading fees and possibly more short-term capital gains taxes. Also, leveraged funds have negative alpha due to their expense ratios. For example, UPRO’s expense ratio of 0.95% translates to a daily alpha of -0.0038%. For the above example, a 25.9% allocation to UPRO would contribute an alpha of -0.00098% (25.9% of -0.0038%), which is very small compared to BND’s alpha contribution of 0.0142% (74.1% of 0.0191%). An Illustration With UPRO and BND Time to put my money where my mouth is. Let’s look at growth of $100k for various target betas achieved by combining SPY with BND, and by combining UPRO with BND. For beta of 0.1, I rebalance whenever the effective beta goes outside 0.075-0.125; for beta of 0.25, 0.2-0.3; for beta of 0.5, 0.45-0.55; for beta of 0.75, 0.7-0.8; and for beta of 0.9, 0.85-0.95. I deduct $7 for each trade (i.e. $14 per rebalance) and assume BND has a beta of -0.035 throughout. (click to enlarge) Performance metrics are given below. Table 1. Performance metrics for SPY/BND and UPRO/BND portfolios with various target betas. Beta Funds Trades Final Bal. ($1k) CAGR (%) Sharpe MDD (%) Alpha (%) 0.10 SPY/BND 3 140.7 5.6 0.116 4.2 0.00018 UPRO/BND 33 143.2 5.8 0.113 4.7 0.00019 0.25 SPY/BND 3 156.4 7.3 0.109 4.2 0.00015 UPRO/BND 35 162.7 8.0 0.110 5.1 0.00018 0.50 SPY/BND 3 183.1 10.1 0.080 8.1 0.00009 UPRO/BND 82 197.5 11.4 0.090 7.7 0.00015 0.75 SPY/BND 2 214.8 12.9 0.068 12.9 0.00005 UPRO/BND 125 237.4 14.7 0.078 12.0 0.00013 0.90 SPY/BND 0 236.7 14.6 0.064 16.9 0.00001 UPRO/BND 153 264.2 16.6 0.074 14.9 0.00011 It makes sense that we see better performance with UPRO/BND with increasing target beta. The greater the target beta, the more we have to allocate to SPY in the SPY/BND portfolio, and the less alpha we retain from the BND allocation. UPRO allows us to allocate more to BND and thus utilize more of its alpha. Risks There are some reasons for caution when trading leveraged funds. I want to briefly re-iterate similar points as in my recent article, A Simple SPY Top-Off Portfolio . If SPY has an intraday loss greater than 33.33%, you could lose your entire balance in the leveraged ETF. UPRO and other leveraged S&P 500 ETFs have historically done an excellent job achieving their target multiple, but there is no guarantee they will continue to do so going forward. In between rebalancing periods, you can suffer some irrecoverable losses due to volatility decay. I would add that the strategy presented in this article uses leveraged funds, but only to achieve a net portfolio beta somewhere between 0 and 1. In that sense, some of the concerns normally associated with leveraged funds do not apply here (e.g. extreme volatility and potentially catastrophic drawdowns). Conclusions The “bonds” part of a stocks and bonds portfolio reduces risk. But so would cash. The reason we prefer bonds is that they generate positive alpha, which improves risk-adjusted returns. Typically, a stocks and bonds portfolio utilizes only a fraction of the bond fund’s alpha. An easy way to increase that fraction is to use leverage. Historical data for UPRO and BND support the notion that using a leveraged fund in place of SPY allows you to capture more a bond fund’s alpha, thus improving both raw and risk-adjusted returns.

Avoiding The Big Drawdown: Is Downside Protection Helpful Or Heresy?

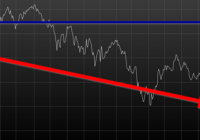
By Wesley R. Gray, Ph.D. Chasing the Investing Unicorn: Give me “High Returns with Limited Risk” Having your cake and eating it too is a great way to go. It’s great to have the cake, and it’s also great to eat the cake. But you can’t have it both ways. This trend continues when we speak with fellow investors: “Give me high, after-tax, net of fee returns, but with limited risk and volatility.” Now, we certainly love high returns with low risk. We also love high reward with low effort and high calories with low weight gain. Unfortunately, this brings us to our first problem with the investing unicorn: Problem #1: Unicorns don’t exist, and neither do high returns with low risk. Unless you are my youngest daughter, age 3, unicorns don’t exist. Sadly, high-return assets with low-risk profiles don’t exist either. Assets that earn high returns, such as equities (e.g., an S&P 500 index fund), come with a lot of risk (i.e., you can lose over half your wealth). The only way to earn high returns, but limit the risk, is to develop a timing methodology that identifies how to sell the high-returning asset before it decides to jump off a fiscal cliff. Which brings me to another kink in the high-reward, low-risk paradox: Problem #2: Market-timing is extremely difficult. Let’s start this conversation with a concise summary of a 55-page academic analysis of a variety of systems that claim to have perfect market-timing ability: Trying to perfectly time the market is a waste of time. There you go. You no longer need to read this classic academic paper in which Ivo Welch and Amit Goyal assess market timing variables. Our own research over several years confirms this sad reality. We’ve reviewed hundreds of different concepts, and the results are not promising. Most signals never “survive” intense empirical scrutiny, and we are generally skeptical of ANY system that purports to work all the time. Simply stated: Nothing works ALL the time . If unicorns don’t exist (high returns, low risk), is there any good news? There is a glimmer of light at the end of this investing tunnel. Specifically, academic research indicates that investors who can stomach short-term volatility, avoid benchmark comparison, and follow a model can systematically outperform over long periods of time. We find the same conclusion with what we call “downside protection.” Historically, two elements provide downside protection: Focus on Strong Absolute Performance Focus on Strong Trending Performance Of course, past performance is certainly no guarantee of future performance ; nonetheless, historically, these methodologies have worked. They haven’t eliminated short-term volatility, and one can be sure they will underperform a buy-and-hold index at some point; however, they have protected portfolios from the most extreme loss situations. Let’s explore a simple downside protection tool and what the evidence to-date can show us. Rule 1: If weak absolute performance appears, go to cash. In the illustration below, the white line represents an asset class with poor absolute performance. In general, avoid assets with poor absolute performance. (click to enlarge) For illustration purposes only. Rule 2: If weak trending performance appears, go to cash. In the illustration below, the purple line represents a long-term trend line (e.g., a moving average) and the white series represents real-time prices. The red circle highlights a point where the real-time price falls below the long-term average. In general, avoid assets with poor trending performance. For illustration purposes only. Do these simple tools work? Let’s look at the data. Moskowitz, Ooi, and Pedersen, in a formal academic paper, highlight that technical rules don’t work all the time, but they have been effective at providing downside protection, historically: “We document significant ” time series momentum ” in equity index, currency, commodity, and bond futures for each of the 58 liquid instruments we consider… … A diversified portfolio of time series momentum strategies across all asset classes delivers substantial abnormal returns with little exposure to standard asset pricing factors and performs best during extreme markets.” – Moskowitz, Ooi, and Pedersen (2012) While market timing systems that work 100% of the time are impossible, we see that some systems, if followed over long periods, can work over time. It all gets back to model discipline and exploiting the behavioral biases of the market (something we love). Let’s simplify the complex analysis presented in formal academic research and focus on replicating these 2 simple rules. Let’s call our system, the “Downside Protection Model”: The Downside Protection Model ((NYSE: DPM )) follows two simple rules: Time Series Momentum Rules (TMOM) Simple Moving Average Rules (MA) Let’s review the details of our simple rules: Absolute Performance Rule: Time Series Momentum Rule (TMOM) Excess return = Total return over past 12 months less return of T-Bills If Excess return > 0, go long risky assets. Otherwise, go long alternative assets (T-Bills) Trending Performance Rule: Simple Moving Average Rule (MA) Moving Average (12) = Average 12-month prices If Current Price – Moving Average (12) > 0, go long risky assets. Otherwise, go long alternative assets (T-Bills). We need a way to combine these two principles in a simple way. We find that complexity does not add value , and simple models beat experts. We extend this belief to downside protection by keeping it simple: We create a Downside Protection Model (DPM) rule, which is 50 percent Absolute Performance (TMOM) and 50 percent Trending Performance (MA): DPM Rule: 50% TMOM, 50% MA Below is a figure that illustrates the basic trading rules we apply to provide downside protection on portfolios: (click to enlarge) The rule is simple: Trigger one rule = go to 50% cash. Trigger both rules = go to 100% cash. No rules triggered = go long. How has the Downside Protection Model performed? We provide a series of tests on the Downside Protection Model, applied to generic market indices. Our core samples includes 5 asset classes, assessed over the 1973-2014 time period: SPX = S&P 500 Total Return Index EAFE = MSCI EAFE Total Return Index LTR = The Merrill Lynch 10-year U.S. Treasury Futures Total Return Index REIT = FTSE NAREIT All Equity REITS Total Return Index GSCI = S&P GSCI Total Return CME Results are gross, no fees are included. All returns are total returns and include the reinvestment of distributions (e.g., dividends). Data sources include Bloomberg. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Comparison #1: Looking at these basic rules individually: Absolute Performance (TMOM) vs. Trending Performance (MA) Before we compare the system as a whole, let’s compare each rule against the other to see if one is particularly more effective. From January 1, 1976 through December 31st, 2014, here is what we find: TMOM wins 60% of the time, MA wins 40% of the time (Win = better Sharpe and Sortino; Loss = Sharpe and Sortino worse; Tie = a combination of some sort) TMOM triggers around 20% less than MA does (number of triggers refers to the number of times the rule breaks out of the asset class and goes to T-Bills) Bottom Line: Both rules have been effective at providing downside protection. Below are the stats. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Comparison #2: Assess the Downside Protection Model (DPM): Absolute Performance (TMOM) plus Trending Performance (MA) Now, let’s combine the rules into our simple Downside Protection Model ( DPM ) and see if any incremental improvement occurs. Here is what we find: Downside Protection Model (DPM) wins overall (Win = better Sharpe and Sortino; Loss = Sharpe and Sortino worse; Tie = combination of some sort). Bottom Line: Combining the rules into a single Downside Protection Model (DPM) appears to work. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Note: Additional robustness tests are available in the appendix. Are these results sustainable? The basic results above highlight that DPM significantly reduces the realized maximum drawdown on a portfolio. But perhaps the entire exercise above is an example of data mining and over-optimization. Nobody can ever prove, beyond any doubt, that a Downside Protection Model works. There is always a chance that any historical finding is driven by randomness, and thus, past performance will not reflect future performance. In the Appendix section below, we stress test this system across numerous time periods and different markets, all of which present similar conclusions. However, we believe there is a behavioral story underlying the success of our simple downside protection rules. Consider the concept of dynamic risk aversion, which is the idea that human beings don’t stick to a set risk/reward behavior – their appetite for risk can change depending on their recent experience. For example, imagine we are making a decision to build a new house in California along the San Andreas Fault. If we just lived through an earthquake, taking on the risk of building a new house on the San Andreas Fault is probably scarier, even though the probability of another earthquake may not have changed. In contrast, when there hasn’t been an earthquake in fifty years, building a new house along a fault is not a big deal. As this example shows, our perception of risk is not constant, and can change based upon recent experience (if you doubt this example, kindly look at a picture of San Francisco’s skyline). In terms of market crashes, we will likely overreact to extreme times and underreact to peaceful times, despite the statistical probability to the contrary. Another assumption economists sometimes make is that risk, often measured in terms of standard deviation, or “volatility,” is relatively constant. These assumptions are challenged when extreme stock market drawdowns occur. Let’s look at another example: a 50% market correction, when fundamentals imply a 20% correction is sufficient. As market prices drop below the twenty percent threshold, an economist assumes that the new price is a bargain. Expected returns have gone up after prices have moved down, while volatility and risk aversion are assumed to be relatively constant. Implicitly, investors should swoop in to buy these cheap shares and bring the market to equilibrium (which, in our example, is their so-called fundamental value). But this doesn’t happen. Stocks can – and have – gone down over fifty percent, and these movements are much more volatile than the underlying dividends and cash flows of the stocks they represent! Remember 2008/2009? How many investors swooped in to buy value versus threw the baby out with the bathwater and kept selling? One approach to understanding this puzzle is by challenging the assumption that investors maintain a constant aversion to risk. Consider the possibility that investors change their view on risk after a steep drawdown (i.e., they just lived through an earthquake). Even though expected returns go up dramatically, risk aversion shoots up dramatically as well. This change means prices have to go down a lot further to justify an investment in these “cheap” stocks. This heightened aversion to risk – following a steep price drop – leads to more selling, and more selling leads to even more hate for risk, which leads to more selling, and so forth. What you end up with is a stampede for the exit and an intense sell-off in the marketplace – below fundamental value, and well beyond what a traditional economist would consider “rational.” The discussion above is a simplified story of investor psychology in the context of a stock market drawdown. For exposition purposes, we are leaving out many potentially important details. However, if one believes that investors rethink their tolerance for risk during a market debacle and tend to sell shares at any price, this might help explain why long-term trend-following rules, which systematically get an investor out of a cliff-diving bear market before everyone has jumped ship, have worked over time. Of course, technical rules will only work if the massive bear market doesn’t happen in a short time period before the long-term trend rules can signal an exit. Technical rules will not save an investor from a 1987-type “flash” crash, but they can save an investor from a 1929- or a 2008-type crash, which can take a few months to develop. In the end, if one believes in a price dynamic that involves steep and relatively sharp declines, followed by slow grinding uphill climbs, simple technical rules will, by design, improve risk-adjusted performance. Conclusion Simple timing rules, focused on absolute and trending asset class performance, seem to be useful in a downside protection context. Our analysis of the downside protection model (DPM), applied on various market indices, indicates there is a possibility of lowering maximum drawdown risk, while also offering a chance to participate in the upside associated with a given asset class. Important to note, applying the DPM to a portfolio will not eliminate volatility, and the portfolio will deviate (perhaps wildly) from standard benchmarks. For many investors, these are risky propositions and should be considered when using a DPM construct. Note: We will be implementing a version of our downside protection model with our new automated advisor offering, Alpha Architect Advisor . Appendix Robustness test of the DPM model across time periods and markets Subperiod: 01/01/1976-12/31/1995 DPM is 50% invested in a TMOM strategy and 50% invested in an MA strategy. Strategies invest in T-bills when a trading rule triggers. DPM wins 3/5, B&H wins 1/5, DPM ~ B&H 1/5 (Win = Sharpe & Sortino; Loss = Sharpe & Sortino; Tie = other) Bottomline: TMOM and MA provide downside protection. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Subperiod: 01/01/1996-12/31/2014 Bottom Line: DPM holds and provides better protection. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Out of Sample Test #1-> U.S. Market (01/01/1928-12/31/1975) Our core sample includes 1 asset class, assessed over the 1928-1975 time period: SPX = S&P 500 Total Return Index Results are gross, no fees are included. All returns are total returns and include the reinvestment of distributions (e.g., dividends). Data sources include Bloomberg. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Both TMOM and MA work well for downside protection, significantly lowering total drawdowns. Strategies invest in T-bills when a trading rule triggers. Bottomline: TMOM and MA provide downside protection and have similar results to the Downside Protection Model. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Drawdown Comparison Both TMOM and MA significantly lower downside risk when the top drawdowns of the buy-and-hold benchmark occurs. MA and TMOM provide similar drawdown protection during buy-and-hold drawdowns. TMOM and MA protect capital at different times (see bold text below). Bottomline: Downside Protection Model diversifies risk management by combining the rules. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Out of Sample Test #2 -> Japanese and German Stock Markets Our robustness samples include 2 global markets (Japan and Germany): NKY = Nikkei 225 Index (1971 to 2014) DAX = Deutsche Boerse AG German Stock Index (1961 to 2014) Results are gross, no fees are included. All returns are price returns and DO NOT include the reinvestment of distributions (e.g., dividends). Data sources include Bloomberg. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. We use zero as the alternative asset return when a trading rule is triggered. Nikkei Summary Results (1971-2014): Both TMOM and MA work well on drawdown protection. TMOM works slightly better overall. TMOM has the highest return during this period. DPM lowers the sum of total drawdowns by a material amount. NKY_DPM (TMOM and MA): Equal weight on NKY_TMOM and NKY_MA; portfolio earns zero returns when flat. NKY_TMOM: Times series momentum applied on NKY with 12-month formation window, and earns zero returns when flat. NKY_MA: 1-month and 12-month MA rule applied on NKY and earns zero returns when flat. NKY_B&H: Buy and hold on Nikkei 225 price-only series. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Drawdown Comparison (Nikkei) Both TMOM and MA significantly lower downside risk during the top drawdowns of the buy-and-hold benchmark. MA and TMOM provide similar drawdown protection during buy-and-hold drawdowns. TMOM and MA protect capital at different times (see bold). The Downside Protection Model is diversifying risk management. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. DAX Summary Results (1961-2014) Both TMOM and MA work well on drawdown protection. TMOM has higher CAGR and lower drawdown. The Downside Protection Model is roughly equivalent to TMOM with lower Max Drawdown. DAX_50,50 (TMOM and MA): Equal weight on DAX_TMOM and DAX_MA; portfolio earns zero returns when flat. DAX_TMOM: Times series momentum applied on DAX with 12-month formation window and earns zero returns when flat. DAX_MA: 1-month and 12 month MA rule applied on DAX and earns zero returns when flat. DAX_B&H: Buy and hold on DAX 40 price-only series. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Drawdown Comparison (NASDAQ: DAX ) Both TMOM and MA significantly lower downside risk during the top drawdowns of the buy-and-hold benchmark. MA and TMOM provide similar drawdown protection during buy-and-hold drawdowns. TMOM and MA protect capital at different times (see bold). The Downside Protection Model is diversifying risk management. (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Statistics Definitions CAGR: Compound Annual Growth Rate Standard Deviation: Sample standard deviation Downside Deviation: Sample standard deviation, but only monthly observations below 41.67 bps (5%/12) are included in the calculation. Sharpe Ratio (annualized): Average monthly return minus Treasury bills divided by standard deviation Sortino Ratio (annualized): Average monthly return minus Treasury bills divided by downside deviation Worst Drawdown: Worst peak-to-trough performance (measured based on monthly returns) Mathematical Relationship Between TMOM and MA (click to enlarge) The results are hypothetical, are NOT an indicator of future results, and do NOT represent returns that any investor actually attained. Indexes are unmanaged, do not reflect management or trading fees, and one cannot invest directly in an index. Additional information regarding the construction of these results is available upon request. Original Post