Why Optimal Portfolios Are So Difficult To Create
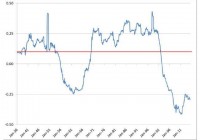
Harry Markowitz won a Nobel Prize in Economics in 1990 for his work on a theory of portfolio management for individual wealth holders. Since that time, Modern Portfolio Theory (MPT) has become the bedrock for creating best-practice portfolio selection methods. Creating an optimal portfolio consists of estimating a portfolio’s future risk and expected return as accurately as possible, based on a variety of inputs. It’s that “as accurately as possible” qualifier that makes the exercise a substantial challenge. MPT requires an investor (or his or her portfolio manager) to: Input expected asset class returns. Estimate the covariances between asset classes, or equivalently, the standard deviations and estimated correlations among asset classes. Decide on portfolio constraints, meaning the limits on the amount going into each asset class. Investors can then compare potential optimal asset allocations for the level of risk they are seeking for their overall portfolio. While there is extensive literature on MPT, accurately projecting an optimal portfolio forward strikes me as nearly impossible. The problem is the estimates. What goes into forecasting an optimal asset allocation has a big impact on what comes out. This often results in suggested optimal allocations that are quite inaccurate, and may lead to portfolio decisions that are counter-productive. Most MPT analysis relies on historical return, risk, covariance and correlation, at least as a starting point. We know that past data can be period-sensitive, so these estimates are often adjusted based on subjective input factors. Investors may have broad views of future Federal Reserve interest rate policy or of the future equity risk premium (ERP). This range of opinion can add wide variability to the accuracy of the outcome. Using only historical data for covariance and correlation can lead to large errors in portfolio optimization. For example, the long-term average correlation between US stocks and 5-year Treasury bonds from 1926-2014 has been +0.1 (correlation ranges from +1.0 to -1.0). However, an analysis of rolling correlation shows this average is far from stable. The 10-year correlation passes through +0.1 on rare occasions, but isn’t there for long. Figure 1 highlights the long-term average correlation (red line) between US stock and 5-year Treasury bond returns using monthly data from January 1936 through September 2014, and the rolling 10-year correlations (blue line) over the same period. Correlation is dynamic, not stable. When you measure correlation and how you measure it has a large bearing on the optimization output. Figure 1: Rolling 10-year Correlation of US stocks and 5-year T-bonds (click to enlarge) Source: CRSP Total US market and Treasury data from Dimensional Fund Advisors, figure by Rick Ferri Markowitz acknowledges the problem of using inaccurate correlation estimates for portfolio optimization in a recent paper he co-authored: ” Enhancing Multi-Asset Portfolio Construction Under Modern Portfolio Theory with a Robust Co-Movement Measure ” by Sander Gerber, Markowitz and Punit Pujara. The authors then attempt to address the issue with a more complex approach to estimating this variable. While the analysis is beyond the scope of this article, it’s fair to say that accurately estimating future correlation is a difficult problem for investors who are trying to solve the optimization puzzle. There are other ways to estimate portfolio risk and return that circumvent correlation estimates. One way is to assume there is no efficient frontier . Each asset class used in a portfolio has its own expected risk and return, and a portfolio of asset classes has an expected risk and return based on the weighted average risk and return of each asset class used in the portfolio. There is no assumed benefit from MPT. The weighted average method to estimating a portfolio’s overall risk and return may be a throwback in time, but it is conservative and does eliminate errors from inaccurate asset class covariance or correlation forecasts. You can read more about this method in my book All About Asset Allocation . Portfolio optimization sounds elegant in theory, but using it in practice is another matter. To have a useful outcome, MPT methodology requires an investor to input accurate asset class expected returns, standard deviation, and covariance or correlation among asset classes. That’s a tall order. Perhaps additional research such as the paper mentioned herein will help, but I’m not betting my retirement savings on it. Disclosure: Author’s positions can be viewed here .